Inhaltsverzeichnis
Leere Mengen, Unendliche Mengen, Zahlenmengen
Leere Mengen
Als leere Mengen bezeichnet man Mengen, die keine Elemente enthalten.
Schreibweise: `A={}` oder `A=\emptyset` (durchgestrichene Null)
Beispiel: `B={x|(x<10 \wedge x>16) \wedge x \in \mathbb{N}}=\emptyset` (keine Zahl ist kleiner 10 und größer 16)
Unendliche Mengen
Als unendliche Mengen bezeichnet man Mengen, die unendlich viele Elemente beinhalten.
Schreibweise: Eine besondere Schreibweise gibt es nicht. Bei der aufzählenden Form oder bei Mengendiagrammen werden Auslassungspunkte verwendet.
Beispiel: `C={x|x>10 \wedge x \in \mathbb{N}}={11; 12; 13; ...}`
Zahlenmengen
Natürliche Zahlen
Symbol: `\mathbb{N}`
Aufzählung: `\mathbb{N}={1; 2; 3; 4; 5; …}`
Hinweis: Die `0` gehört nicht zu den natürlichen Zahlen (`0 \notin \mathbb{N}`)
Ganze Zahlen
Symbol: `\mathbb{Z}`
Aufzählung: `\mathbb{Z}={…; -3; -2; -1; 0; 1; 2; 3; … }`
Hinweise: Die natürlichen Zahlen sind eine Teilmenge der ganzen Zahlen (`\mathbb{N} \subset \mathbb{Z}`)
Rationale Zahlen (Gebrochene Zahlen)
Symbol: `\mathbb{Q}`
Beschreibung: `\mathbb{Q}={x/y | x \in \mathbb{Z} \wedge y \in \mathbb{Z} \wedge y \ne 0}`
Hinweise: Die Beschreibung sagt, dass alle Brüche zu den rationalen Zahlen gehören, die als Zähler eine ganze Zahl und als Nenner eine ganze Zahl haben. Dazu muss der Nenner noch verschieden von Null sein.
Irrationale Zahlen
Symbol: `\mathbb{I}` (Ein I (Ihhh) mit doppeltem Strich)
Hinweise: Zu den irrationalen Zahlen gehören alle Zahlen, die sich nicht als Bruch darstellen lassen. Dazu gehören solche Zahlen, wie `sqrt(2)` oder `\pi`. Näher möchte ich darauf nicht eingehen :)
Reelle Zahlen
Symbol: `\mathbb{R}`
Beschreibung: `\mathbb{R} = \mathbb{Q} \cup \mathbb{I}`
Hinweise: Die reellen Zahlen enthalten die gebrochenen Zahlen und die irrationalen Zahlen. Für die „Schulmathematik“ sind das eigentlich „alle“ Zahlen. Das stimmt aber so nicht, da es in der Mathematik noch andere Zahlenmengen gibt, die nicht in der Schule behandelt werden. Siehe zum Beispiel: Komplexe Zahlen.
Zusammenhänge
`\mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R}`
Das bedeutet: Jede natürliche Zahl ist auch eine ganze Zahl. Jede ganze Zahl ist auch eine gebrochene Zahl und jede gebrochene Zahl ist auch eine reelle Zahl.
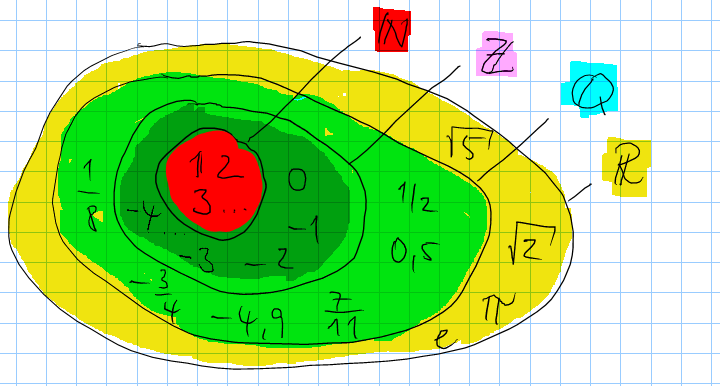
Hinweise:
- `\mathbb{I}` fehlt in der Zeichnung. Aber: `\mathbb{I} = \mathbb{R}\\mathbb{Q}` (Reelle Zahlen ohne die rationalen Zahlen)
- Häufig werden noch zusätzliche Zahlenmengen verwendet:
- `\mathbb{P}`: Menge der Primzahlen (natürliche Zahlen, die nur durch 1 und sich selbst teilbar sind)
- `\mathbb{V}_2`: Menge der geraden natürlichen Zahlen
- `\mathbb{U}`: Menge der ungeraden natürlichen Zahlen
- `\mathbb{N}_0`: Menge der natürlichen Zahlen mit der Null (`\mathbb{N}_0 = \mathbb{N} \cup {0}`)
- `\mathbb{Q}^{+}`: Menge der positiven gebrochenen Zahlen