Aufgaben AK D10/V10
Quadratische Funktionen/Gleichungen
1) Anzahl der Lösungen durch Koeffizienten bestimmen
(LB 9 S. 60/8)
Bestimme die Belegung der Koeefizienten so, dass die Gleichung keine, eine oder zwei Lösungen hat:
| a) $x^2-4x+a=0$ | b) $x^2+ax+12=0$ | c) $(x-a)^2=0$ |
| d) $(x+a)^2=0$ | e) $x^2+7x+a=0$ | f) $x^2-ax+3=0$ |
| g*) $0=2x^2+bx+12$ | h*) $0=2x^2+bx-12$ | i*) |
Hinweise:
Die Diskriminante entscheidet, wie viele Lösungen eine quadratische Gleichung hat. $D=b^2-4ac$
a) $a=1; b=-4; c=a$
$D=(-4)^2-4*1*a=16-4a$
keine Lösung:
$D<0$
$16-4a<0 | +4a$
$16<4a | :4$
$4<a$ $(a>4)$
→ Bei $a>4$ hat die Gleichung keine Lösung. Schau dir das in desmos an! Und so weiter …
2) Muskel-Manfred
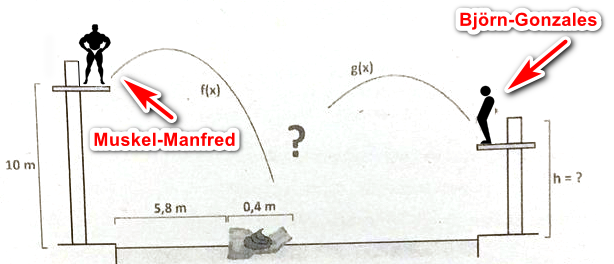
Muskel-Manfred möchte den Frauen im Schwimmbad imponieren. Nach einer Phase des Herumposierens am Beckenrand beschließt er, vom Zehnmeterbrett zu springen. Seine Flugbahn kann durch die Parabel $y=f(x)=- 1/2 x^2 + 3/2 x + 10$ beschrieben werden (1 LE = 1m).
a) Berechne den nöchsten Punk $S$ der Flugbahn.
b) Berechne denjenigen Abstand $x$ vom Sprungbrett, bei dem Manfred eine Höhe von $5m$ besitzt.
Im Bereich des Kinder-Planschbeckens bückst zeitgleich Björn-Gonzales seiner Mutter aus. In einem unbeobachteten Moment entledigt er sich seiner vollen Windel und wirft sie mitten ins Sprungbecken. Die Windel befindet sich im Beeich $5,8 le x le 6,2$.
c) Berechne, ob Manfred in der Gefahrenzone landet.
Ohne den zusätzlichen Balast am Hintern, klettert Björn-Gonzales rasch auf den gegenüberliegenden Sprungturm und pinkelt in hohem Bogen, gemäß der Funktion $y=g(x)=-x^2+19x-85$, ins $10\ m$ breite Becken.
d) Berechne die Höhe $h$, aus der Björn-Gonzales pinkelt.
e) Berechne den Schnittpunkt der beiden Parabeln und entscheide, ob Muskel-Manni schon vor der Landung im Wasser nass wird …
Hinweise: Deine Lösungen kannst du gut in desmos prüfen, in dem du die beiden Graphen richtig interpretierst.
