Wichtig für das Lösen der Aufgaben ist, dass du die Begriffe richtig zuordnen kannst.

In 3d:

Mit der rechten Maustaste drehen! Scrollen mit der Maus zum Zoomen!

• Dreiseitiges Prisma
• Vierseitiges Prisma (hier: Quader)
• Ein lustiges Prisma

Aufgaben:

1. Wonach wird ein Prisma benannt? nach Grund-/Deckfläche, Anzahl der Seiten
2. Wie viele Ecken hat das dargestellte gerade Prisma? 6
3. Wie viele Kanten hat dieses Prisma? 9
4. Welche Kanten sind bei jedem Prisma gleich lang? die Seitenkanten, die nicht zur Grund- oder Deckfläche gehören
5. Wie viele gleich lange Kanten hat das dargestellte gerade Prisma? 3
6. Wie viele Begrenzungsflächen hat dieses gerade Prisma? 5
7. Welche zwei Begrenzungsflächen eines Prismas sind immer deckungsgleich (kongruent)? Grund- und Deckfläche

Eine Schokoladenpackung von 12 cm Länge hat als Querschnittsfläche ein gleichschenkliges Trapez mit a = 6 cm, c = 3 cm, h = 2 cm. Konstruiere das auf der größten Seitenfläche liegende Prisma im Schrägriss (α = 45°, v = ½)!

So:

Ein dreiseitiges Prisma mit der Höhe h = 30 cm hat als Grundfläche ein rechtwinkliges Dreieck mit den Katheten a = 24 cm und b = 20 cm. Berechne das Volumen!

`A_(Grundfläche) = 1/2 * a * b = 0,5 * 24 cm * 20 cm = bb(240 cm^2)`

`V_(Prisma) = A_(Grundfläche) * h = 240 cm^2 * 30 cm = bb(7.200 cm^3)`

Berechne die Mantelfläche des gegebenen Prismas! Gib eine Formel an!

1. Gerades dreiseitiges Prisma: a = b = 7,5 m, c = 13,9 m, h = 18,4m
2. Regelmäßiges sechsseitiges Prisma: a = 35 cm, h = 3,20 m
3. Regelmäßiges achtseitiges Prisma: a = 40 cm, h = 2 cm

Die Mantelfläche sind alle Flächen außer Grund- und Deckfläche.

Es gibt verschiedene Möglichkeiten die Mantelfläche zu berechnen. Die einfachste ist, den Umfang der Grundfläche oder der Deckfläche mit der Höhe des Prismas zu multiplizieren:

zu 1.)

`u_(Grundfläche) = a + b + c = 7,5 m + 7,5 m + 13,9 m = bb(28,9 m)`

`A_(Mantelfläche) = u_(Grundfläche) * h_(Prisma) = 28,9 m * 18,4 m = bb(531,76 m^2)`

zu 2.)

`u_(Grundfläche) = 6 * 35 cm = bb(210 cm)`

`A_(Mantelfläche) = u * h = 2,1 m * 3,2 m = bb(6,72 m^2)`

zu 3.)

`u = 8 * 0,4 m = 3,2 m`

`A = u * h = 3,2 m * 2 m = bb(6,4 m^2)`

Ein 80 cm langer Dreikant hat als Querschnitt ein gleichschenkliges Dreieck mit a = b = 5,5 cm und c = 6 cm. Berechne die Mantelfläche und die Oberfläche des Dreikants!

`A_(Mantel) = u_(Grundfläche) * h_(Prisma)`

`A_(Mantel) = (5,5 cm + 5,5 cm + 6 cm) * 80 cm = bb(1.360 cm^2)`

Es fehlt eine Größe: Die Höhe des Dreiecks der Grundfläche. Diese bekommt man nur durch Messen heraus. Man muss das Dreieck mit Hilfe des Konkruenzsatzes sss konstruieren und die fehlende Höhe messen:

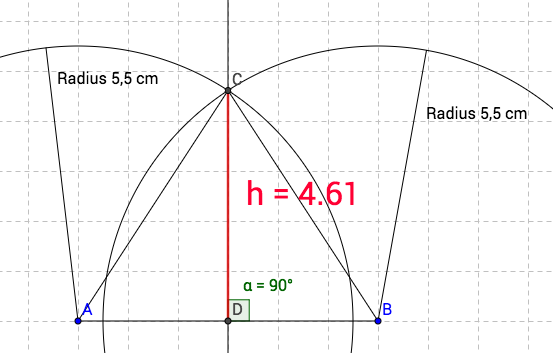
Aus der Zeichnung folg: `h = 4,61 cm`

`A_(Grundfläche) = 1/2 * c * h_c = 0,5 * 6 cm * 4,61 cm`

`A_(Grundfläche) = bb(13,83 cm^2)`

`A_(Oberfläche) = A_(Grundfläche) + A_(Deckfläche) + A_(Mantelfläche)`

`A_(Oberfläche) = 13,83 cm^2 + 13,83 cm^2 + 1.360 cm^2 = bb(1.387,66 cm^2)`

Zwei Seitenflächen einer prismatischen Blumenkiste sind gleichschenklige Trapeze (a = 48 cm, c = 24 cm, h = 32 cm). Die Blumenkiste ist 120 cm lang. Wie viel Liter Erde finden in der Blumenkiste Platz? Wie viel m² Kunststoff sind zur Innenverkleidung notwendig?

Skizze:

`V_(Blumenkiste) = A_(Grundfläche) * l_(Blumenkiste)`

`A_(Grundfläche) = 1/2 * (a+c) * h = 0,5 * (48 cm + 24 cm) * 32 cm = bb(1.152 cm^2 = 11,52 dm^2)`

`V_(Blumenkiste) = A_(Grundfläche) * l_(Blumenkiste) = 11,52 dm^2 * 12 dm = bb(138,24 dm^3 = 138,24 l)`

Innenverkleidung können wir noch nicht.

Die Baugrube für einen Ausstellungspavillion hat die Form eines dreiseitigen Prismas. Von der dreieckigen Grundfläche kennt man die Länge der Seite a = 30 m und die Länge der dazugehörigen Höhe ha = 40 m. Die Höhe des Prismas beträgt h = 6 m. Wie viel m³ Erde müssen ausgebaggert werden?

Skizze:

`V = A_(Grundfläche) * h_(Prisma)`

`A_(Grundfläche) = 1/2 * a * h_a = 0,5 * 30 m * 40 m = bb(600 m^2)`

`V = A_(Grundfläche) * h_(Prisma) = 600 m^2 * 6 m = bb(3.600 m^3)`

Der Flächeninhalt der Grundfläche eines Prismas beträgt 27,8 dm². Das Prisma hat ein Volumen von 180,7 dm³. Berechne die Höhe des Prismas! Forme die Volumsformel geeignet um.

`V = A_(Grundfläche) * h`

oder kürzer:

`V = A * h`

Gesucht ist h. Daraus folgt:

`h = V/A`

`h = (180,7 dm^3)/(27,8 dm^2) = bb(6,5 dm)`